

It is covered with the subject of the Euclidean theorem. Solution 2- (2): The height of the hypotenuse in a right triangle is found by dividing the product of perpendicular sides by the hypotenuse. If k / root5 is written instead of x, since k = 2 root5, then | BC | = 10 cm. In triangle ABC k² = x.kk root5, x = k / root5 from the Euclidean relation. Solution 2- (1): From the Pythagorean relation in ABC triangle | BC | = k.rok5. Solution: In an ABC isosceles triangle (| AC | = | BC |), if a point of the base is D | AD | ² = | AB | ²- | BD |. Question 😎 ABC and KCN are each triangle, perpendicular, | AD | = | KN |, | AK | = | KC | if What is the measure of the KNB angle? Special right triangles test-1 answers Question 7-) ABCD is a quadrilateral, if perpendicular, m (ADC) = 60 °, m (CBA) = 45 °, | AD | = 11 cm, | CD | = 6 cm | BC | how many cm? Question 6-) If ABC is a triangle, | AB | = (root3) -1 cm, m (ACB) = 15 °, m (CBA) = 30 ° | AC | = how many cm is x?
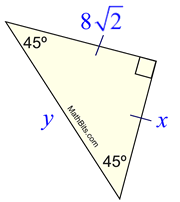
Question 5-) ABC is a triangle, if | AB | = 10 cm, m (BAC) = 15 °, m (ACB) = 135 ° | AC | = how many cm is x? Question 4-) If perpendicular, perpendicular, m (BAD) = 45 °, | AB | + | BC | = 6 cm | AD | how many cm? Question 3-) If ABC right triangle, perpendicular, perpendicular, | BN | ² + | NC | ² = 112 cm², | AN | = 12 cm | BC | how many cm? Question 2-) In right triangle ABC, if perpendicular, | AC | = 2 | AB |, | AD | = 4 cm | BC | how many cm? Question 1-) If ABC is a triangle, | AB | = | AC | = 9 cm, | AD | = 7 cm | BD |. Geometry topics, right triangles, special triangles, 30 60 90 triangle, 45 45 90 triangle, 15 75 90 triangle, 15 30 135 triangle, euclidean, pythagorus, magnificent triangles, special triangle questions according to sides and angles.
Special right triangles 45 45 90 pdf#
That’s it! Once you’ve done these mental steps a few times, it should be fairly easy to close your eyes and come up with the solution in a matter of seconds - and there is really no need to memorize anything! Just apply the Pythagorean Theorem, and it’s very quick to see that you need to get 1/2 + 1/2 = 1 once you’re done squaring things.Geometry subjects special right triangles test-1 answers and PDF … Therefore, in a right triangle with a 45 degree angle, if the hypotenuse is 1, then the legs are both the square root of 1/2. And the value of “?” that satisfies ? + ? = 1 is clearly 1/2.

And a triangle with two equal angles must have two equal sides, so - guess what? - the legs of the triangle are equal. Time to get clever: since one of the acute angles is 45 degrees, the other one must be as well (how else can you get 180 degrees?).
Next we go ahead and square things, giving this: To find out, we apply the Pythagorean Theorem, and we get this: We are dying to find out how long the legs are. For convenience, let the hypotenuse have length 1. We start with a right triangle with a 45 degree angle. Here is my effort to make it as simple as possible to “see” what these values should be, without having to resort to memorization. To all those studying trigonometry - let’s take the mystery out of special right triangles, shall we? In a trig class, students are expected to know the sine and cosine of angles that are 45 degrees, or perhaps a multiple of 45 degrees.


 0 kommentar(er)
0 kommentar(er)
